
Ocelová lana představují v dnešní době důležitou strojovou součástku v mnoha průmyslových odvětvích. Jsou využívána hlavně v hornictví, stavebnictví a dopravě. Používají se při těžbě surovin v dolech, dopravě lidí, u jeřábů velkých nosností, pro lanové dráhy apod. Základní podmínkou funkce těchto zařízení je nutnost stoprocentního stavu ocelového lana.
Výroba ocelových lan (obr. 1) představuje jednu z nejnáročnějších výrobních operací v průmyslovém odvětví. Způsobuje to zejména fakt, že lano je nosný prvek, na kterém závisí ochrana zdraví lidí a jejich bezpečnost. Ocelová lana tvoří určité základní konstrukční prvky a dělí se do několika skupin. Základní prvky ocelového lana jsou: ocelový drát, pramen a duše.

Obr. 1 Ukázka procesu výroby ocelových lan [1, 2]
Dráty ocelových lan mohou mít různé tvary a průměry, které ovlivňují vlastnosti samotného lana. Ocelové dráty tažené za studena jsou nosnými částmi lana. Tvoří 93–100 % materiálu lana. Zaručují velkou nosnost lana i při relativně malých průměrech a malých hmotnostech. Jsou ohebné, což umožňuje navíjení lana na cívky a jeho ohýbání přes kladky. Potřebné mechanické vlastnosti, jako pevnost v tahu, vhodnou kvalitu a potřebné geometrické rozměry povrchu, získá drát tažením. Průřez drátů ocelového lana může být různý. Pramen lana (obr. 2) je prvek lana složený vinutím drátů a uložený ve stejném směru, v jedné nebo více vrstvách kolem středu. Tvoří ji jaderný drát, kolem kterého jsou skládány další dráty. Ocelová lana prošla několika etapami vývoje od svého vzniku. Každá etapa přinesla nové konstrukce, nové typy ocelových lan, co se týče počtu pramenů, jejich způsobu a směru vinutí, doteku drátů, pevnosti drátů a povrchové úpravy.
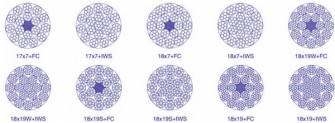
Obr. 2 Příklady různých typů pramenů použitých při konstrukci ocelových lan [3]
Duše ocelového lana představuje velmi důležitou součást lana. Duše je vyrobena z textilních přízí, ale může být i ocelová nebo ocelová opřádaná. Napouští se mazadlem, aby během provozu bylo lano mazané a tím se prodloužila její životnost. Úkolem duše je:
- vytvářet pružnou a pevnou podložku, zabraňující radiálnímu posunutí pramenů a bočnímu tlaku. Duše má od sebe oddělit prameny lana tak, aby se v zatíženém stavu právě jen dotýkaly;
- zásobovat lano během jeho provozu mazadlem, které snižuje tření při posuvech drátů a pramenů mezi sebou. Je velmi důležité, aby se z textilní duše mazadlo dostávalo do míst mezi dráty a prameny;
- vyplňovat prostor mezi prameny a zajistit kruhový průřez lana. [4]
Duše ocelových lan (obr. 3) může být z následujících materiálů:
- ocel ve formě ocelového pramene nebo lana. Tyto duše se používají hlavně v provozech, kde jsou vyšší teploty, které by textilní duše nesnesla a kde hnaný element je uchycen pomocí třecích svorek, kde se vyžaduje menší průměr lana nebo větší nosnost apod.;
- textilní příze, kterou rozdělujeme do dvou skupin, na příze z přírodních materiálů, sisalu, konopí, manily a juty a na přízi z umělých materiálů, polopropylénového štěpného pásku;
- tuhý polymer. Duše sestává z tuhého polymeru kruhového průřezu, nebo z kruhového průřezu s drážkami, může obsahovat i vnitřní prvek, kterým je drát. [4]
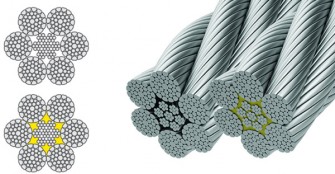
Obr. 3 Příklad různých typů duší ocelových lan [5]
Základní východiska tvorby modelů ocelových lan v CAD programech
Obecně lze problematiku tvorby modelu ocelového lana rozdělit do tří základních kroků. Prvním a zároveň klíčovým krokem je matematické vyjádření osy jednotlivých drátů. Pod matematickým vyjádřením je třeba rozumět odvození vztahů, pomocí kterých bude možné popsat jejich trajektorii. Počet rovnic záleží na konkrétní konstrukci ocelového lana, tzn. kolik má drátů, vrstev, pramenů a jaký je použit typ duše. Příklad jednoduché parametrické rovnice osy drátů ocelového lana může být např. v následující podobě:
x = (s – Rp)*(cos(d)*cos(k*t*360) + sin(d)*sin(k*t*360))*cos(t*360) + (s – Rp)*(cos(d)*sin(k*t*360) – sin(d)*cos(k*t*360))*sin(t*360) + Rp*cos(t*360)
y = (s – Rp)*(cos(d)*cos(k*t*360) + sin(d)*sin(k*t*360))*sin(t*360) – (s – Rp)*(cos(d)*sin(k*t*360) – sin(d)*cos(k*t*360))*cos(t*360) + Rp*sin(t*360)
z = (s – Rp)*sin(b)*(cos(d)*sin(k*t*360) – sin(d)*cos(k*t*360)) + t*360*(pi/180)*Rp*(cos(b)/sin(b)) [7]
Matematická vyjádření hrají při modelování ocelového lana velmi důležitou roli. Určují úhel vinutí jednotlivých drátů v prameni a tím i úhel vinutí celého pramene. To znamená, že dříve, než se začne samotné modelování, je třeba mít k dispozici správné matematické vyjádření pro všechny komponenty.
V rámci druhého kroku je třeba odvozené matematické vztahy vhodným způsobem definovat ve zvoleném CAD systému a jejich pomocí vymodelovat osy jednotlivých drátů. Tento krok opět není jednoduchý, protože definování matematických vztahů v jednotlivých CAD programech se výrazně liší a následná tvorba os může rovněž představovat oříšek. Po zvládnutí této fáze je možné přejít k vytvoření konečného modelu ocelového lana prostřednictvím tvorby partů jednotlivých drátů a následným vyskládáním celého finálního modelu v režimu tvorby sestav.
V další části příspěvku bude ve stručnosti popsána tvorba jednoduchého modelu ocelového lana ve třech různých CAD softwarech. Ve všech třech CAD softwarech byl realizován stejný model ocelového lana SEAL 6x (1 + 9 + 9) + v.
Tvorba modelu ocelového lana v PTC Creo Elements
Pro tvorbu modelů ocelových lan, jak již bylo zmíněno, je třeba mít matematické vyjádření os jednotlivých drátů, které se v programu v PTC Creo Elements zpracovávají pomocí „Menu Manager“. Následně proces tvorby pokračuje použitím volby „From Equation“. Ze souřadnicového systému v pracovním okně se vybere příslušný souřadnicový systém, např. „PRT_CSYS_DEF!, a v okně „Menu Manager“ se upřesní jeho typ na „Cartesian“.
Po potvrzení operace v okně „CURVE: From Equat...“ se v pracovním okně zobrazí křivka, která znázorňuje tvar a směr vinutí budoucího drátu. Přes volbu „Create or edit sweep section“ se nakreslí kruhový profil drátu, který musí mít střed v bodě, kde se protíná horizontální a vertikální osa. Tento bod představuje výchozí bod osy drátu. Pro dokončení tvorby drátu se využije možnost „Sweep as solid“ a operace se potvrdí pomocí „Apply and saves any changes...“, čímž se dokončilo modelování prvního drátu. Stejným způsobem se vymodelují i zbylé dráty ocelového lana. V závěrečné fázi modelování se v modulu pro tvorbu sestav vyskládá z jednotlivých drátů finální model ocelového lana (obr. 4).
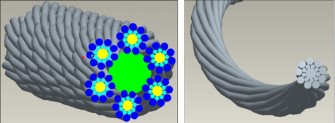
Obr. 4 Výsledný model ocelového lana vytvořený pomocí CAD programu Creo Elements
Modelování ocelového lana v Solidworks
Tvorba modelu ocelového lana je na rozdíl od předchozího postupu trochu komplikovanější. Dříve než se začne modelovat ocelový drát, je třeba mít k dispozici parametry pro souřadnice bodů „x, y, z“, které definují trajektorii jeho osy. Program Solidworks nemá možnost přímého zadávání matematických funkcí křivek a zároveň samostatně nespočítá úhly ze stupňů na radiány, proto je na tyto úkony potřebné použít vhodný externí program, např. Microsoft Excel. Jeho pomocí se přepočítají všechny matematické vztahy a do Solidworks se budou vkládat pouze samotné parametry pro „x, y, z“. Jelikož se modeluje lano, které obsahuje v jednom prameni 9 vnitřních, 9 vnějších drátů a duši pramene, je třeba realizovat tyto výpočty pro každý jeden drát a duši zvlášť.
Následně je třeba hodnoty parametrů „x, y, z“ překonvertovat do poznámkového bloku, kde se nejprve nahradí všechny čárky tečkou a následně všechny mezery čárkami. Pak se soubor uloží s příponou CSV. Aby Solid Works dokázal číst dané hodnoty, je třeba tuto příponu souboru přepsat na příponu .sldcrv. Tyto kroky je třeba zopakovat pokaždé u všech drátů. Pomocí položky „Curve through XYZ Points...“, která se nachází v položce „Insert“, se zvolí uložený soubor s příponou .sldcrv a následně se otevře (obr. 5).
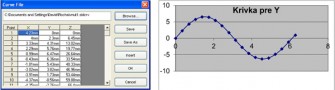
Obr. 5 Okno „Curve File“ s parametry pro první drát a graf vygenerovaných souřadnic osy y ocelového lana
Potvrzením operace se vytvoří křivka pro budoucí drát. Po označení této křivky je třeba nakreslit profil drátu. V záložce „Tools“ se zvolí „Sketch Entities“ a vybere se tvorba kružnice. Kruhový profil drátu se musí nacházet na konci křivky, a tak počáteční hodnoty pro „x“ a „y“ budou vždy nulové. Určí se požadovaný průměr drátu a operace se potvrdí. Pomocí funkce „Swept Boss/Base“ se namodeluje drát s průměrem po celé délce křivky (obr. 6). Následně se celá operace potvrdí. Tímto způsobem se postupně vymodelují všechny dráty vnitřní a vnější vrstvy. Důležité je, že přes položku „Curve through XYZ Points...“ se stále musí zadávat souřadnice bodů „x , y , z“ pro daný drát , který se modeluje. Znamená to, že u každého drátu se tyto parametry budou měnit.
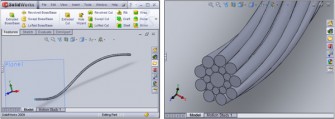
Obr. 6 Postup tvorby modelu ocelového lana v programu Solidworks
Pro vymodelování pramene je třeba otevřít pracovní prostředí „Assembly“, které slouží pro tvorbu sestav. Funkcí „Browse“ se otevře první model, který představuje duši. Následně se otevře další model pomocí položky „Existing Part/Assembly...“, která se nachází v záložce „Insert Component“. Zapletení těchto komponent do sebe umožňuje funkce „Mate“. Je však třeba v produktovém stromu ztotožnit roviny zvolením si „Origin“ u obou komponent, které se automaticky zapletou do sebe. Pro dokončení tohoto procesu je třeba potvrdit operaci.
Stejně se postupuje i při otevírání a skládání všech ostatních komponent. Důležité však je, že jedna z rovin bude stále představovat rovinu stejného modelu, která tvoří základní rovinu pro samotnou sestavu. V tomto případě je to duše. Druhá rovina je stále rovina modelu, která se aktuálně spojuje se sestavou. Tímto způsobem se vymodeluje kompletní sestava, která představuje pramen ocelového lana s duší.
Při modelování ocelového lana se použije pracovní prostředí „Assembly“, ve kterém se využije funkce „Pattern“. V první řadě je třeba mít vytvořen a uložen pramen a duši lana. Nejjednodušší způsob „patternování“ je, že se bude dále pracovat s pramenem, který se před chvilkou vytvořil, a nebude se otevírat uložený pramen.
Je třeba vytvořit osu, kolem které se budou „patternovat“ prameny lana. Samotná osa se nachází pod položkou „Reference Geometry“ v záložce „Insert“. Po označení „Axis“ je třeba označit roviny „Right“ a „Top“. Následně se operace potvrdí, čímž se vytvořila osa.
Samotné „patternování“ je velmi jednoduché. V záložce „Insert“ se zvolí položka „Component Pattern“ a vybere se možnost „Circular Pattern“. V první řadě se zvolí osa, pak se změní úhel na 60 stupňů (modeluje se šestipramenné lano) a v okně se vybere počet pramenů, což představuje 6 kusů. Následně je třeba postupně si označit všechny části pramene, všechny dráty a také duši. Po potvrzení operace se vytvořilo šestipramenné ocelové lano bez hlavní duše.
Duše ocelového lana se vymodeluje podobným způsobem jako v Pro/Engineerovi nebo Catii V5. V první řadě se vymodeluje válec příslušného průměru a následně se po úpravě matematických vyjádření vymodeluje každý jeden drát zvlášť. V dalším kroku je třeba „patternovat“ všechny dráty a pomocí funkce „Sweep cut“ se tyto dráty odeberou z vymodelovaného válce.
Pro konečné vymodelování lana se použije pracovní prostředí „Assembly“, kde se pomocí funkce „Browse“ otevře první model, který představuje vymodelovaná duše lana. Následně se klikne na položku „Existing Part/Assembly“ nacházející se v záložce „Insert Component“, pomocí které se otevřou a vloží ostatní komponenty lana. Tímto způsobem se „poskládají“ všechny vymodelované části a vytvoří tak hotové ocelové lano.
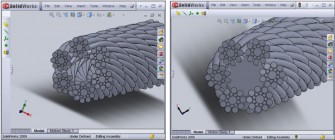
Obr. 7 Výsledný model ocelového lana v programu Solidworks
Tvorba modelu ocelového lana v Catii
Modelování v programu Catia V5 neprobíhalo stejným způsobem jako v předchozích programech. V Creo Elemets a Solidworks byly nejprve vytvořeny všechny komponenty pramene lana. Následně se pramen poskládal přes funkci „Assembly“ a až potom následovalo „patternování“ pramene na potřebný počet pramenů v lanu.
V programu Catia V5 se „patternuje“ každý jeden komponent pramene ihned (obr. 9) po vymodelování do potřebného počtu a při konečném skládání lana se tak modelovaly všechny prameny současně. Modelování samotné duše ocelového lana je velmi složitý a náročný proces z hlediska počtu kliknutí a také z časového hlediska. Při modelování duše je nutné znovu definovat matematické vyjádření a znovu vymodelovat všechny komponenty pramene, které se musí „patternovat“ (obr. 8). Následně se tyto vymodelované díly odeberou pomocí různých funkcí programu (Remove, Sweep Cut) z vymodelovaného válce s průměrem duše, který představuje budoucí duši lana.
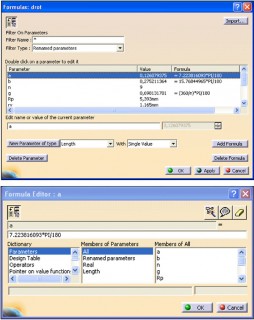
Obr. 8 Okna pro zadávání parametrů, veličin a matematických vztahů
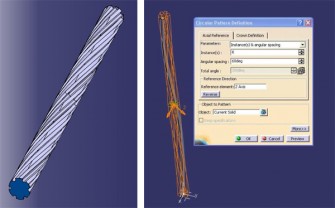
Obr. 9 Model duše ocelového lana v programu Catia a patternování drátů
Porovnání tvorby modelů ocelových lan
Před samotným porovnáváním modelování ocelového lana v jednotlivých softwarech bylo v prvé řadě třeba určit kategorie a veličiny, které se budou sledovat, měřit a srovnávat, aby konečný výsledek byl objektivní a pravdivý.
Při modelování ocelového lana bylo třeba mnohokrát kliknout myší na okna, položky a příkazy. Při měření počtu kliknutí byly stanoveny stejné podmínky pro všechny programy, například do měření se počítalo i kliknutí v souvislosti se samotným otevřením softwaru, pracovního prostředí, či kliknutí při modelování a ukládání modelů. Je třeba uvést, že u všech programů se vycházelo ze skutečnosti, že byla k dispozici všechna matematická vyjádření a u Solidworks i hodnoty souřadnic bodů „XYZ“ pro všechny komponenty pramene. Modelování v programu Catia V5 neprobíhalo stejným způsobem jako ve zbývajících programech.
V Creo Elemets a Solidworks byly nejprve vytvořeny všechny komponenty pramene lana. Následně se pramen poskládal přes funkci „Assembly“ a až potom následovalo „patternování“ pramene na potřebný počet pramenů v laně. V programu Catia V5 se „paternoval“ každý jeden komponent pramene ihned po vymodelování do potřebného počtu a při konečném skládání lana se tak modelovaly všechny prameny současně.
Modelování samotné duše ocelového lana je velmi složitý a náročný proces z hlediska počtu kliknutí a také z časového hlediska. Při modelování duše je nutné znovu definovat matematické vyjádření a znovu vymodelovat všechny komponenty pramene, které se musí „patternovat“. Následně se tyto vymodelované díly odeberou pomocí různých funkcí programů (Remove, Sweep Cut) z vymodelovaného válce o průměru duše, který představuje budoucí duši lana.
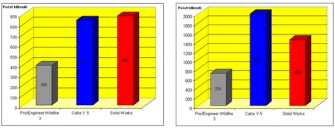
Obr. 10 Přehled počtu kliknutí potřebných k vymodelování ocelového lana
Z grafu je vidět, že nejmenší počet kliknutí při modelování ocelového lana bez duše se realizoval při modelování v Creo Elements, pak následovala Catia V5 a Solidworks.
V programech Creo Elements a Catia modelování ostatních drátů trvalo mnohem kratší dobu než modelování prvního drátu z důvodu, že všechny vztahy na začátku jsou definovány a upraveny tak, že stačí měnit hodnotu parametru „i“ a všechny nově vytvořené dráty budou pootočené vzhledem k předchozímu drátu. V případě Solidworks je třeba modelovat každý jeden drát zvlášť, což představuje stále stejný počet kliknutí. Při vkládání matematických vyjádření byl naměřen největší počet kliknutí u programu Catia V5 z důvodu, že bylo třeba nadefinovat každou jednu veličinu a každý jeden matematický vztah v modelu. Tyto operace nevyžadovaly programy Creo Elemets a ani Solidworks. Po vymodelování kompletního ocelového lana byl nejmenší počet kliknutí naměřen v programu Creo Elements zejména zásluhou jednoduchého modelování. Následoval program Solidworks a největší počet kliknutí byl naměřen v programu Catia V5, hlavně z důvodu náročné práce s matematickými vyjádřeními.
Využití vytvořených CAD modelů
Uvedené porovnávání možností modelování ocelových lan bylo realizováno z důvodu výběru vhodného, nejrychlejšího a nejjednoduššího způsobu tvorby geometrických modelů ocelových lan pro potřeby jejich FEM analýzy pomocí programu Abaqus (obr. 11).

Obr. 11 Příklad výpočtu ocelového lana pomocí geometrického modelu vytvořeného v programu Catia
Každý z programů nabízí výhody, které je možné využít pro konkrétní specifické konstrukce ocelových lan. Z praktických zkušeností z práce s uvedenými softwarovými nástroji je možné konstatovat, že pro modelování některé konstrukce ocelového lana je vhodnější jeden a pro jinou zase jiný CAD systém.
Závěr
Proces modelování ocelového lana je složitý postup, který se liší ve všech programech v závislosti na propracovanosti daného programu. V některých softwarech je 3D modelování ocelového lana z důvodu jeho konstrukce ztížené, jiné programy to zvládají s velmi vysokou kvalitou, ale samotný proces modelování je u každého programu jedinečný.
Cílem příspěvku bylo popsat modelování ocelového lana ve třech různých CAD softwarových balících. Modelování probíhalo ve všech programech velmi podobným způsobem, avšak určité odlišnosti při modelování, z důvodu některých nedostatků programů, nás nutily práci mnohokrát předělávat.
Po vymodelování ocelového lana v programech Creo Elements, Catia V5 a Solidworks byly jednotlivé postupy tvorby modelu podrobeny detailnímu srovnání. Programy se porovnávaly z hlediska počtu kliknutí myší při modelování, času trvání modelování, náročnosti práce s matematickými vyjádřeními, celkové náročnosti modelování a samozřejmě i celkového dojmu z programu a modelování v něm.
Po porovnání programů bylo zjištěno, že se nedá jednoznačně určit program, který je nejvhodnější pro modelování ocelového lana. Nejvhodnější program, který představuje „vítěze“ porovnávání, se totiž mění v závislosti na tom, zda se bere v úvahu konstrukce lana, čas, práce a náročnost počáteční transformace matematických vyjádření a výpočty hodnot souřadnic bodů „x, y, z“.
Článek je součástí řešení grantových projektů VEGA 1/0922/12, VEGA 1/0036/12, APVV SK-CZ-2013-0169 a KEGA 006STU-4/2015.
Literatura
1. https://encrypted-tbn3.gstatic.com/images?q=tbn:ANd9GcRbfggWQzQ4WxYcttieO3ngHznhsEY5aZ3EOOnDvdzXdxglwG_S
2. http://www.wireandtubenews.com/wp-content/uploads/2012/11/Rope-onto-Take-Up-Stand-Bridon-Neptune-Quay-300x195.jpg
3. https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcTL7sZXh2DJofQ88Fe1APTEfVl8VUxwCOb9J2YaCCB5JBY5VBpMgw
4. Molnár, V. a kolektiv: Oceľové laná. Vydala Fakulta BERG, Technická univerzita v Košiciach, Košice, 2006, s. 200, ISBN 80-8073-629-4
5. http://www.lrwmagazine.com/wp-content/uploads/2015/08/4.png
6. Fabian, M. – Spišák, E.: Navrhování a výroba s pomocí CA.. technologií. 1. vyd. Brno: CCB, 2009. 398 p. ISBN 978-80-85825-65-7.
7. Stanová, E.: Geometry and Modeling of Oval Strand of n0+(2n0+4)+n2 Type. In: SSP – Journal of Civil Engineering, Selected Scientific Paper, Vol. 7, Issue. 2 (2012), pp. 33–40. DOI: 10.2478/v10299-012-0004-3
