Snižování nákladů bylo vždy aktuální téma. Někdy však vede k určité standardizaci procesů, což má za následek omezení v oblasti inovací. U vývoje výrobku naopak optimalizace přímo inovaci podporuje. Při použití moderních nástrojů dokážou firmy snížit náklady na vývoj výrobků pomocí virtuálního testování – simulace. Tím se výrazně redukují náklady vznikající při vytváření fyzického prototypu a snižuje se čas uvedení výrobku na trh. Některé společnosti dokonce fyzické prototypy z vývojového procesu zcela odstranily. Dalším příkladem je tvarová optimalizace, která přináší úsporu materiálu a snížení hmotnosti výrobku, při zachování požadovaných parametrů.

Společnost IDIADA, distributor softwaru Abaqus v ČR a na Slovensku, pořádá pro své zákazníky, ale i širší odbornou veřejnost pravidelné semináře zaměřené na optimalizaci při vývoji výrobku. Přednášejícími jsou vývojoví pracovníci společnosti IDIADA, kteří čerpají z vlastních zkušeností a projektů, ale také R&D manažeři a specialisté z řad zákazníků a uživatelů softwaru Abaqus. Na posledním semináři jsme se zabývali nelineárními materiály – především plasty a gumou.

Plasty a jejich simulace

Množství používaných výrobků z plastů s sebou přináší požadavek dimenzovat tyto výrobky. Jednou z možností je využití metody konečných prvků. Ani ten nejpřesnější výpočetní model neposkytuje věrohodné výsledky, pokud je použit nevhodný materiálový model nebo nepřesné materiálové parametry. Obvykle bývají plasty popisovány v případě lineárních výpočtů pomocí elastických konstant – modulu pružnosti v tahu a Poissonovy konstanty v případě izotropního a homogenního materiálu. Co ale v případě, když se výrobek výrazně deformuje anebo když je výrobek dlouhodobě zatížen např. při zvýšené teplotě? V takovýchto případech si již nevystačíme s jednoduchým lineárním výpočtem, kde napětí je přímo úměrné zatížení.

Obvyklý způsob popisu nelineárního chování plastového materiálu je pomocí elasto-plastického modelu (tedy stejného, který se používá pro houževnaté oceli). V první řadě je nutné si rozmyslet způsob a podmínky zatěžování – v jakých podmínkách bude díl pracovat – plasty většinou vykazují významnou závislost na teplotě, rychlosti zatížení (náraz nebo dlouhodobé působení)...

Pro určení materiálových vlastností je nutné provést měření na zkušebních tělesech – většinou tahové zkoušky dle ISO norem. Následně je nutné z naměřených dat odvodit materiálové parametry ve formě, kterou požadují MKP systémy. Proces odlaďování přináší jistá úskalí, je třeba jisté zkušenosti pro dosažení přesného výsledku. Tato fáze byla zevrubně popsána na únorovém semináři.

Pro plast můžeme použít elasto-plastického materiálového popisu, ale není to ten nejpřesnější způsob, ač je nejpoužívanější. Abaqus nově nabízí přesný nelineární model, který kombinuje elasticitu definovanou pomocí hyperelastického modelu (možno redukovat na lineárně elastický) v kombinaci s časově závislým viskózním členem.

Sériovým řazením těchto dvou členů – elastického a viskózního – vzniká tzv. Maxwellův model. Pokud paralelně zkombinujeme tyto Maxwellovy modely, můžeme velice přesně popsat chování libovolného plastu – jak polymeru, tak elastomeru. Viskózní složka musí postihovat i závislost na velikosti zatížení, která může být značně nelineární – čím více se blížíme s napětím mezi kluzu, tím výrazněji se projevuje náchylnost materiálu na tečení. Do tohoto modelu můžeme zakomponovat další doplňkový paralelní člen – elasto-plasticitu. Tímto můžeme zpřesnit např. popis chování plastu při cyklickém zatěžování.

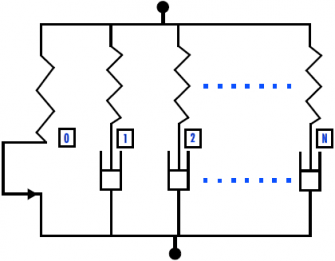
Obr. 1 Reologické schéma nelineárního viskoelastického modelu

Teplotní závislost viskoelastického modelu můžeme definovat pomocí jednoduchého termo-reologického chování definovaného pomocí Williams-Landel-Ferry (WLF) vztahu a Arrheniusova vztahu – zde definujeme „posun" mechanických vlastností v závislosti na aktuální teplotě. Lze použít také uživatelských subrutin, kde můžeme „posun" definovat podle libovolného vztahu pro každý Maxwellův model zvlášť (větev modelu).

Simulace gumových materiálů

Pryž přírodní nebo syntetická je dnes již dobře známý a hojně používaný materiál, který má díky svým unikátním vlastnostem nezastupitelné místo v průmyslových aplikacích, se kterými přicházíme denně do styku. Namátkou vyberme obuv, pneumatiky, hadice, těsnění, ochranné pomůcky, dopravníky, ale třeba i oděvy.

Uplatnění v průmyslu je tedy široké a firmy zabývající se návrhem pryžových výrobků řeší zejména problémy spojené s optimalizací rozměrů, tvarů a hmotnosti současně se zachováním nebo zlepšením mechanických vlastností výrobku a jeho životnosti. Cestu, jak dospět k optimálnímu designu, má každá vývojová firma svou vlastní a nezastupitelnou roli v ní mají finančně i časově nákladné fyzické prototypy a jejich testování v laboratořích. U nás v IDIADA jdeme při vývoji nových produktů cestou snižování počtu fyzických prototypů, které nahrazujeme prototypy virtuálními, nebo chcete-li, numerickým modelováním.
U pryže si při modelování mechanického chování produktu nevystačíme s jednoduchými vztahy ze strojnických tabulek pro výpočty tuhosti nebo deformace. Je to proto, že tyto vztahy byly odvozeny za předpokladu malých deformací a lineárního izotropního „hookovského" materiálu, jakým je ocel.

V případě pryží se potřebujeme pohybovat v oblasti velkých deformací a současně potřebujeme popsat vysoce nelineární vztah napětí–deformace. Zde nastupuje dnes již dobře známá a prověřená metoda konečných prvků, v našem případě implementována v softwaru Abaqus. Práce potom probíhá dle jednoduchého schématu.

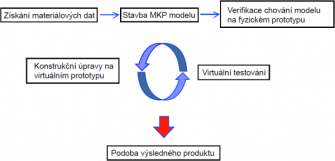
Získávání materiálových dat

Základním předpokladem pro dobře fungující virtuální prototyp jsou kvalitní materiálová data. Při jejich získávání postupujeme od nejjednodušších a nejlevnějších materiálových testů s tím, že rozsah a podmínky testování volíme s ohledem na výslednou aplikaci produktu.

Pokud nás zajímá například jednoduchá statická tuhost silentbloku motoru, vystačíme si s jednoduchým měřením tvrdosti dle normy Shore-A, na základě něhož jsme schopni jednoduše a rychle („za dopoledne") naladit materiálový model pryže, který bude dobře popisovat mechanické chování při deformacích materiálu v rozsahu desítek procent.

Chceme-li však modelovat dynamické chování pneumatik za různých teplot, pak nás čekají podstatně náročnější testy jedno- a víceosých tahových a tlakových charakteristik při různých teplotách a rychlostech zatěžování.

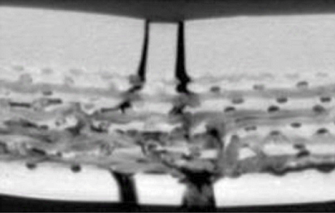
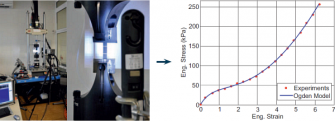Obr. 2 Jednoosá tahová zkouška pryže

Od požadované aplikace se ostatně odvíjí také volba materiálového modelu. V Abaqusu je standardně obsažena většina známých a prověřených materiálových modelů popisujících hyper-elastické chování pryžových materiálů (Neo-Hook, Mooney-Rivlin, Ogden, Arruda-Boyce, Yeoh, Van der Waals atd.).

Jednodušší modely se hodí pro simulace menších deformací, zatímco pokročilejší modely nám budou dobře popisovat chování pryžového dílu i při extrémním namáhání. Pro jejich spolehlivé naladění však pochopitelně budeme potřebovat rozsáhlejší a nákladnější měření.

Abaqus se však neomezuje pouze na popis hyper-elastického chování, ale věnuje se i dalším fenoménům, kterými se pryž vyznačuje:

• (ne)stlačitelnost pryže – Obecně se pryž chová jako nestlačitelný materiál, v některých extrémních případech se však projevuje minimální stlačitelností. V Abaqusu se dá (ne)stlačitelnost jednoduše definovat a modelovat tak chování charakteristické pro danou aplikaci.
• Mullinsův efekt – Je to degradační jev, který způsobuje porušování některých typů molekulových řetězců při deformaci pryžového dílu. Pryžová součást, která již jednou byla deformována, si tuto deformaci „pamatuje" a vykazuje nižší tuhost nežli součást nová. Tento jev je významný například při změně chování nového pryžového dorazu a dorazu, který už byl někdy použit.
  
  
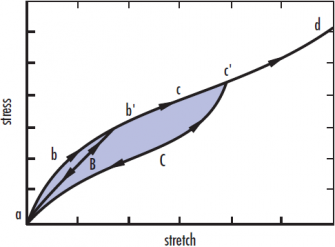  Obr. 3 Změna napjatosti v závislosti na historii zatěžování
  
  
• Creep – neboli „tečení" materiálu je pozvolný děj, ke kterému dochází pod konstantním zatížením. Tedy pokud zavěsíme břemeno na pryžový závěs, tak postupem času dojde k jeho postupnému protažení. Je to důsledek visko-elastického chování, stejně jako pokles napětí v předepnuté pryžové pružině, kterému říkáme Relaxace napětí.
• Hystereze – je děj, který popisuje změnu mechanické energie na energii tepelnou. To nás zajímá, pokud například potřebujeme sledovat ztráty energie v dynamické soustavě, jakou je například odvalující se pneumatika.
• Rychlostně závislé chování – nás bude zajímat zejména při vyšších rychlostech zatěžování, kdy dochází k tzv. zpevňování materiálu. Pryž tedy vykazuje podstatně vyšší tuhost nežli při statickém zatěžování. Toto je typické například pro dopadání břemen nebo bariérové zkoušky.
  
  
  
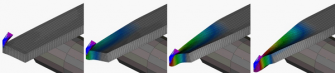
  Obr. 4 Simulace a experiment dopadu břemene na pásový dopravník

Shrnutí – proč používat Abaqus a simulace obecně?

Abaqus nabízí rozsáhlou paletu nástrojů, kterými je možné simulovat komplexní chování pryžových materiálů, kdy se navíc nesoustřeďujeme pouze na jeden fenomén, ale kombinujeme současně více podstatných vlastností v jednom modelu. Z praxe víme, že tyto simulace vykazují vysoký stupeň shody s reálnými experimenty, je to však podmíněno kvalitními vstupními daty a pečlivě zvolenými a odladěnými materiálovými modely. V takovém případě je Abaqus velmi silným a robustním nástrojem, který nám umožňuje:

• Minimalizovat počet vyrobených prototypů,
• minimalizovat počet reálných zkoušek například pro účely certifikace,
• sledovat děje uvnitř struktury materiálu, které jsou obtížně měřitelné nebo prakticky neměřitelné – např. smyk mezi vrstvami kordu v pneumatice při dálničním provozu,
• zrychlit vývojový cyklus,
• prověřit větší množství konstrukčních variant.

Další téma: výpočet životnosti

V příštím semináři se zaměříme na další odborné téma – životnost. Díky nové akvizici společnosti Safe Technology, která vyvíjí produkt FE-SAFE, doplňuje Abaqus v portfoliu SIMULIA krom jiných také tento produkt.

Proč potřebujeme výpočet životnosti? Nevystačíme si s výpočtem napjatosti? Jsou situace, kdy výpočet životnosti je nezbytný, a to v případě, že zatížení probíhá v cyklech. Je všeobecně známo, že právě cyklická povaha zatěžování nám výrazně snižuje „dovolené" napětí. Životnostní výpočet nám umožní kvantifikovat důsledky zvýšení počtu/druhů cyklů. Dále nám výpočet umožňuje zjistit počet cyklů do vzniku trhliny v materiálu nebo faktor bezpečnosti – kolikrát lze zvýšit napětí, než dojde ke vzniku trhliny.

Vstupními hodnotami jsou:

• Vypočtené hodnoty napětí z MKP modelu. Většinou je vypočtena lineární statická odezva na jednotkové zatížení a výsledný průběh zatížení je dodefinován v softwaru na výpočet životnosti. Můžeme využít superpozici jednotlivých směrů – výsledný signál zatížení pak může mít jak amplitudu / střední hodnotu časově závislou, tak orientace tohoto zatížení se může s časem měnit (mluvíme pak o obecném trojosém zatížení).
• Vstupní signál (např. průběh zatížení, kterým definujeme jeden cyklus). Vstupní signál lze skládat z bloků, které mohou být libovolně kombinovány.
• S–N křivka známá jako Wöhlerova křivka – závislost napětí do porušení vers. počet cyklů. Pro nízko-cyklovou životnost se používá E–N křivka (přetvoření vers. počet cyklů). Tyto křivky jsou získávány pro jednoosé cyklické zatížení.
• Pokud naše zatížení je jiné než ideálně cyklické, je nutné volit algoritmus, který koriguje střední hodnotu napětí. Pokud je střední hodnota zatížení rovna nule, jedná se o střídavé zatížení (pro které jsou změřeny S–N křivky).

Pomocí tohoto modulu životnosti můžeme počítat životnost nejenom pro statické chování, ale i rychlé dynamické vibrační chování.

Životnostní výpočty lze využít nejen pro ocel, litinu, hliník, ale i méně obvyklé materiály pro tento způsob dimenzování, jako guma, kompozitní materiály, ocele za vysokých teplot.

Zaujalo vás toto téma? Chcete také vyvíjet výrobky efektivně a snižovat náklady? Přijměte naše srdečné pozvání na další seminář, který se uskuteční 12. června 2013 v Praze. Více informací najdete na www.idiada.cz.

Použité zdroje:

1. Uživatelský manuál SIMULIA Abaqus
2. Webové stránky výrobce: www.3ds.com/products-services/simulia/overview/