V článku „CAD systémy a plechové autíčko" byl v minulém čísle představen projekt autíčka z plechu, které je vyráběno v jednom z exponátů akce Steelpark – kreativní fabrika [1]. V článku byl popsán návrh tvaru karosérie autíčka a podvozku, jakož i vizualizace pracoviště s využitím současných CAD systémů. Po navržení tvaru karosérie bylo třeba zamyslet se nad způsobem výroby karosérie a ověřit její vyrobitelnost zvolenou technologií.

Současná doba poskytuje možnosti posouzení výrobních procesů již v předvýrobní etapě bez existence reálných nástrojů i strojů, a to využitím počítačové podpory inženýringu (inženýrských činností) – Computer Aided Engineering (CAE). Software zaměřený na tuto oblast umožňuje na simulačním modelu ověřit navrhovaný proces – deformaci materiálu při tváření, pohyb nástroje při obrábění, tok plastu při jeho vstřikování do formy apod. Proces probíhá ve virtuálním prostředí simulačních programů s využitím CAD modelů navržených nástrojů a definovaných okrajových podmínek konkrétní technologie. Numerická simulace tedy využívá simulační model vytvořený jako umělý (virtuální) objekt a simuluje jeho chování v určitých specifických podmínkách na základě matematického popisu samotného procesu a materiálových charakteristik [2].

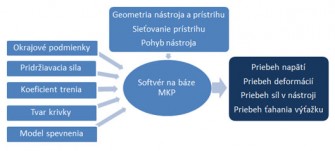Obr. 1 Vstupy a výstupy simulačních programů hlubokého tažení na bázi MKP

Simulační softwary pro technologické procesy jsou založeny na metodě konečných prvků – MKP, (resp. FEM – Finite Element Method). Při analýze metodou MKP těleso, které ve skutečnosti představuje nekonečný počet bodů, je rozděleno na velký počet samostatných dílů – konečných prvků (nodes). Následně jsou podle okrajových podmínek na tyto prvky aplikovány výpočetní rovnice. Hraniční body těchto prvků, případně některé další významné body, jsou uzlovými body, ve kterých se určují neznámé hodnoty posuvů hran prvků vytvářejících síť. Hustota konečnoprvkové sítě je rozhodující pro přesnost výsledků [2, 3].

Pro výrobu karosérie autíčka byla zvolena technologie hlubokého tažení v tažném nástroji s přidržovačem. U návrhu koncepce tvářecích nástrojů jsou kromě teoretických znalostí důležité i praktické zkušenosti, které je třeba uplatnit při navrhování geometrie funkčních částí, odstupňování jednotlivých operací, výpočtu sil, určení polohy a tvaru brzdicích žeber, velikosti a tvaru výchozího polotovaru, volbě mazadla apod. Ověřování variantních řešení výroby výlisku tradiční experimentální cestou vyžaduje zhotovení reálných nástrojů (u velkých rozměrů výlisku ve vhodném měřítku podle zákona podobnosti – geometrické, materiálové, fyzikální), z čehož vyplývají vysoké náklady a značná časová náročnost [4, 5, 6].

Vyrobitelnost výtažků složitých tvarů z plechů technologiemi plošného tváření závisí v podstatné míře na tvářitelnosti použitého materiálu a na správné volbě technologických podmínek lisování. Numerická simulace umožňuje předvídat vliv materiálových vlastností, geometrie výtažku a nástroje, jakož i vlastností mazadla na technologické charakteristiky tvářitelnosti tak, aby bylo možné v maximální míře využít vlastnosti materiálu a zároveň i možnosti technologie jeho zpracování – obr. 1.

Simulační přístup byl použit i při návrhu výroby karosérie autíčka z obalového plechu (obr. 2). Jako vstupní materiál byl použit ocelový obalový plech z produkce U. S. Steel Košice. Numerickou simulací v simulačním softwaru PAM-STAMP 2G byly ověřovány okrajové podmínky – vhodnost tvaru a geometrie funkčních částí tažného nástroje (tažník, tažnice a její poloměr zaoblení), jakost a tloušťka plechu, velikost přidržovací síly a tvar výchozího polotovaru.

Obr. 2 CAD model výlisku karosérie

Obr. 3 Části nástroje a polotovar síťované v simulačním programu PAM-STAMP 2G

PAM-STAMP 2G je simulační program využívající metodu konečných prvků, v němž jsou prvky výpočtu zobrazovány ve formě sítě (mesh). Pro části, které se nedeformují, např. funkční části nástroje, představuje síťování popis geometrie a využívá se pro definování kontaktních podmínek (tření). Na druhé straně, síťovaný polotovar představuje malé elementy materiálu s předepsanými vlastnostmi, které jsou důležité z hlediska plastické deformace – model zpevnění, podmínka plasticity, normálová anizotropie apod. [7].

Základem pro numerickou simulaci tažení karosérie je 3D model funkčních částí nástroje vytvořený v libovolném CAD systému. Postup jejich vytvoření byl popsán v předchozí části článku. Tento 3D model je pro potřeby numerické simulace vhodné upravit tak, aby vzájemná poloha tažníku a tažnice určovala konečnou pozici při lisování, při respektování směru tažení v kladné ose Z. Tyto části jsou exportovány do neutrálního souboru ve formátu IGS, který slouží pro přenos geometrických dat nástroje do simulačního programu.

Obr. 4 Zkoušené tvary přístřihů

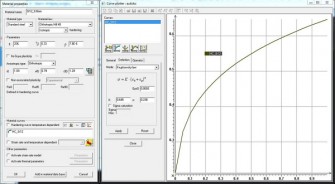
Obr. 5 Definování materiálového modelu – výběr podmínky plasticity, určení křivky
zpevnění a normálové anizotropie Lankfordovými koeficienty

Velmi důležitým krokem je příprava konečnoprvkové sítě nástroje, tedy síťování (meshing). V simulačním programu PAM-STAMP 2G je síťování realizováno při importu CAD dat z formátu IGS do simulačního programu v modulu DeltaMESH. Síťování je však možné realizovat i v samostatných CAD programech a pak importovat do simulačního programu přímo vytvořenou síť jednotlivých funkčních částí nástroje. Síťované plochy činných částí nástroje pro výrobu karosérie plechového autíčka jsou znázorněny na obr. 3 (pro názornost nejsou jednotlivé díly v konečné poloze).

V dalším kroku bylo nutno vytvořit tvar polotovaru včetně definování jeho materiálových vlastností. Tvary přístřihů použitých v simulacích jsou znázorněny na obr. 4. Tvar přístřihu byl odvozen pomocí makra Blank editor z obrysové křivky polotovaru po jeho importu do simulačního programu. Současně byl přístřih rozdělen (síťován) na konečnoprvkovou síť s parametry, které lze měnit podle požadavků uživatele. Důležité jsou zejména velikost prvků a úroveň zjemnění síťování během výpočtu. Pro popis materiálu je třeba v simulačním softwaru zadat následující vstupní údaje:

• Základní materiálové charakteristiky – měrná hmotnost, Youngův modul pružnosti, Poissonova konstanta;
• Podmínku plasticity určující přechod z elastické do plastické oblasti v závislosti na poměru hlavních napětí;
• Křivku přirozeného deformačního odporu, která definuje zpevňování materiálu při plastické deformaci (tzv. model zpevnění);
• Lankfordovy koeficienty ve směrech 0°, 45° a 90° pro popis normálové anizotropie plechu.

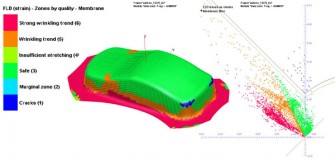Obr. 6 Výsledek numerické simulace – materiál TS 275, tloušťka 0,2 mm

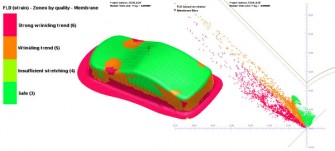
Obr. 7 Výsledek numerické simulace – materiál TS 245, tloušťka 0,3 mm

U numerické simulace hlubokého tažení karosérie plechového autíčka byl využit materiálový model z databáze aplikace PAM-STAMP 2G, který se svými vlastnostmi nejvíce přibližoval vlastnostem použitých obalových pocínovaných plechů. Materiálový model St12 byl popsán izotropním modelem zpevňování s podmínkou plasticity Hill48, normálovou anizotropií definovanou Lankfordovými koeficienty ve směrech 0°, 45° a 90° vzhledem ke směru válcování a Krupkowského modelem zpevňování materiálu – obr. 5.

Pro výrobu karosérie plechového autíčka bylo uvažováno s jakostmi obalového plechu TS 275 o tloušťce 0,2 mm a TS 245 o tloušťce 0,3 mm. Při použití obalového plechu TS 275 o tloušťce 0,2 mm byl výsledek simulace neúspěšný i při změně přidržovací síly a variování poloměru zaoblení tažné hrany tažnice. Zobrazení výtěžku karosérie plechového autíčka a diagram mezních deformací pro posouzení porušení výtažku jsou na obr. 6. Následně byl použit materiál TS 275 o tloušťce 0,3 mm, u kterého byly stanoveny parametry přidržovací síly 10 kN, poloměr zaoblení tažnice 1 mm a tvar polotovaru podle obr. 4 vpravo. U simulací byly podmínky tření definovány součinitelem tření f = 0,2, což odpovídá hranici suchého a polosuchého tření, protože při tažení nebylo uvažováno s použitím mazadla. Výsledek simulace pro materiál TS 245 o tloušťce 0,3 mm je uveden na obr. 7. Postup vytváření karosérie plechového autíčka je uveden na obr. 8.

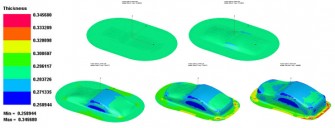Obr. 8 Etapy tažení karosérie plechového autíčka (změna tloušťky)

Simulační programy a jejich využití při návrhu technologie výroby konkrétní součástky mají v současnosti významné místo. Jak je patrné z uvedeného příkladu, poskytují technologovi – konstruktérovi nářadí silný nástroj pro ověření vyrobitelnosti navrhovaného tvaru výrobku zvolenou technologií, včetně možnosti optimalizace tvaru vstupního polotovaru, technologických podmínek výroby a jakosti použitého materiálu. Zároveň však kladou na technologa – konstruktéra nářadí požadavek na teoretické znalosti navrhované technologie, které jsou vedle schopnosti ovládání příslušného softwaru nezbytnou podmínkou pro maximální využití možností navrhované technologie. Je však třeba poznamenat, že výsledek numerické simulace je pouze tak přesný, jak přesně jsou naměřena vstupní materiálová data. Problematika matematického popisu materiálových modelů zpevnění, podmínek plasticity, kontaktních poměrů při hlubokém tažení a mezních křivek deformací je vysoce aktuální ve výzkumu současných vysokých škol, výzkumných pracovišť a společností, které vyvíjejí a poskytují podporu pro simulační programy hlubokého tažení.

Článek vznikl s podporou projektu VEGA 1/0500/12 „Výzkum zlepšování kvality frézování tvarových ploch pokročilými povlakovanými nástroji" a projektu VEGA 1/0396/11 „Výzkum a optimalizace metod hodnocení pevnostních a plastických vlastností velmi tenkých obalových plechů".

Literatura

• [1] Projekt plechového autíčka pre Steelpark. [on-line]. Košice: TU, SjF [cit. 2013-06-14]. Dostupné na internetu
• [2] Spišák, E.: Matematické modelovanie a simulácia technologických procesov – ťahanie. TYPO Press Košice: 2000. 156 s. ISBN 80-7099-530-0
• [3] Hrivňák, A. – Evin, E.: Lisovateľnosť plechov. Košice: Elfa, 2004. – 223 s.: ISBN 80-89066-93-3
• [4] Evin, E. – Élesztos, P. – Petrmichl, R. – Kmec, J.: CAE podpora pri navrhovaní výroby výliskov. Transfer inovácií, 9/2006, s. 73–76, ISSN 1337-7094
• [5] Kováč, P. – Tittel, V.: Blank holder force optimization of hemispherical product using numerical simulation. In: Materials science and technology. No. 5 (2010), pp. 5–10, ISSN: 1335-9053
• [6] PAM-STAMP 2G & PAM-TUBE 2G User's Guide, ESI Group, 2009